BFS (Breadth-First Search)와 DFS (Depth-First Search)는 그래프와 트리 탐색에 널리 사용되는 두 가지 알고리즘이다.
각 알고리즘의 개념과 차이점을 간단히 정리해보자.
1. BFS (Breadth-First Search):
- 개념: BFS는 너비 우선 탐색으로, 시작 노드에서부터 가까운 노드들부터 탐색을 진행하는 것이다.
- 탐색 방식: 큐(Queue)를 사용하는 방식이고, 시작 노드를 큐에 넣고, 큐에서 노드를 하나씩 꺼내며 인접한 노드를 모두 큐에 넣는 방식이다.
- 용도: 최단 경로 찾기, 레벨 순회 등.근처 탐색에 유리하다.
- 특징: 모든 간선의 가중치가 동일할 때 최단 경로를 찾을 수 있습니다.
2. DFS (Depth-First Search):
- 개념: DFS는 깊이 우선 탐색으로, 한 노드의 자식 노드를 끝까지 탐색한 후 다음 노드를 탐색한다.
- 탐색 방식: 스택(Stack)이나 재귀(Recursion)를 사용한다. 시작 노드에서 자식 노드를 탐색하고, 자식 노드의 자식 노드를 계속 탐색하는 방식이다.
- 용도: 경로 탐색, 사이클 검출 등. 멀리있는 것을 탐색하는데 유리하다.
- 특징: 모든 경로를 탐색하기 때문에 경로의 깊이를 우선으로 탐색하는 것이다..
| 특징 | BFS | DFS |
| 자료구조 | 큐 | 스택/재귀 |
| 탐색 우선 순위 | 너비 우선 | 깊이 우선 |
| 최단 경로 | 예 (모든 간선의 가중치가 동일할 때) | 아니요 |
| 적용 분야 | 최단 경로, 레벨 탐색 | 경로 탐색, 사이클 검출 |
이렇게 BFS와 DFS는 각각의 장점과 단점을 가지고 있어서, 문제의 성격에 따라 적절한 알고리즘을 선택해야 한다.

BFS 와 DFS 코딩할때 노드로하면 느려도 터지진않는다!
재귀함수로 하면 실행 과정에서 스택에 쌓이기때문에 스택 오버플로우의 위험이 있다.
즉 너무많이 사용하면 펑!
조금 느린대신 엥간해선 터지지않는 노드탐색으로 만드는게 베스트 인듯하다!
아래는 c# 기반 DFS ,BFS 코드이다.
using System;
using System.Collections.Generic;
namespace Day22
{
//원래 링크드 리스트에선 노드가 넥스트 하나만 있었지만.
//비선형에선 다음 노드들을 여러개 가지고있다.
public class Node<T>
{
public T Value { get; set; }
public List<Node<T>> Neighbors { get; private set; }
public Node(T value)
{
Value = value;
//
Neighbors = new List<Node<T>>();
}
}
//노드들 관리
public class SimpleGraph<T>
{
List<Node<T>> _nodes = new List<Node<T>>();//노드들을 관리하는 리스트(공간) 뉴할당.
//노드 추가기능
public Node<T> AddNode(T value)
{
Node<T> node = new Node<T>(value);//여기서 노드의 뉴할당 진짜 값들은거
_nodes.Add(node);
return node;
}
//노드와 노드의 연결선을 엣지라 부를거임.
//단방향 간선 추가
public void AddEdge(Node<T> from, Node<T> to)
{
//출발점의 노드가 가진 리스트에, 목적지 노드 추가
from.Neighbors.Add(to);
}
//양방향 간선 추가
public void AddUndirectedEdge(Node<T> from, Node<T> to)
{
from.Neighbors.Add(to);
to.Neighbors.Add(from);
}
public void PrintGraph()
{
foreach (var node in _nodes)
{
Console.Write($"{node.Value} -> ");
foreach (var neighbor in node.Neighbors)
{
Console.Write($"{neighbor.Value} ");
}
Console.WriteLine();
}
}
//BFS = B Fisrst Search ->너비 우선 탐색
//큐를 사용해 탐색할거임
//시작 노드를 큐에 담고 탐색을 시작함
public void BFS(Node<T> strat, Node<T> target)
{
Queue<Node<T>> queue = new Queue<Node<T>>();
List<Node<T>> visited = new List<Node<T>>();//방문기록용 //중복체크용
queue.Enqueue(strat);
while (queue.Count > 0)
{
Node<T> current = queue.Dequeue();
if (visited.Contains(current))//내가 방문했던곳에서 현재꺼가있다면 다시
{
continue;
}
Console.WriteLine($"{current.Value}");
visited.Add(current);
if (current.Equals(target))
{
Console.WriteLine($"목적지 {target.Value}도달");
return;
}
foreach (var neighbor in current.Neighbors)
{
//방문한적이 없다면 q에 추가해줌
if (!visited.Contains(neighbor))
{
queue.Enqueue(neighbor);
}
}
}
Console.WriteLine("경로 탐색 실패");
}
//DFS = Depth Fisrst Search ->깊이 우선탐색
public void DFS(Node<T> strat, Node<T> target)
{
Stack<Node<T>> stack = new Stack<Node<T>>();
List<Node<T>> visited = new List<Node<T>>();//방문기록용 //중복체크용
stack.Push(strat);
while (stack.Count > 0)
{
Node<T> current = stack.Pop();
if (visited.Contains(current))//내가 방문했던곳에서 현재꺼가있다면 다시
{
continue;
}
Console.WriteLine($"{current.Value}");
visited.Add(current);
if (current.Equals(target))
{
Console.WriteLine($"목적지 {target.Value}도달");
return;
}
foreach (var neighbor in current.Neighbors)
{
//방문한적이 없다면 q에 추가해줌
if (!visited.Contains(neighbor))
{
stack.Push(neighbor);
}
}
}
Console.WriteLine("경로 탐색 실패");
}
}
internal class Program
{
static void Main(string[] args)
{
SimpleGraph<string> graph = new SimpleGraph<string>();
var nodeA = graph.AddNode("천호역");
var nodeB = graph.AddNode("암사역");
var nodeC = graph.AddNode("강동구청역");
var nodeD = graph.AddNode("강동역");
var nodeE = graph.AddNode("길동역");
var nodeF = graph.AddNode("광나루역");
//8호선
//graph.AddEdge(nodeA, nodeB);
graph.AddUndirectedEdge(nodeA, nodeB);
//graph.AddEdge(nodeA, nodeC);
graph.AddUndirectedEdge(nodeA, nodeC);
//5호선
//graph.AddEdge(nodeE, nodeD);
graph.AddUndirectedEdge(nodeE, nodeD);
//graph.AddEdge(nodeD, nodeA);
graph.AddUndirectedEdge(nodeD, nodeA);
//graph.AddEdge(nodeA, nodeF);
graph.AddUndirectedEdge(nodeA, nodeF);
//출력
graph.PrintGraph();
//BFS = B Fisrst Search ->너비 우선 탐색
//DFS = Depth Fisrst Search ->깊이 우선탐색
graph.BFS(nodeA, nodeE);
}
}
}
아래는 BFS 의 천호역 출발 길동역 도착 탐색이다.
그리고 DFS 로 바꿔서 출력 했을 경우
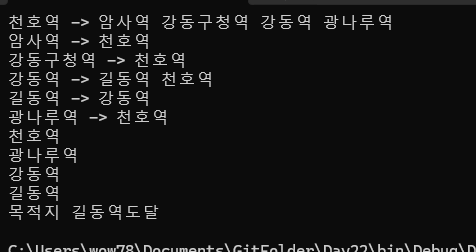
아래처럼 조금 짧아졌다.
이처럼 길찾기 처럼 목표가 명확한 경우는 DFS 즉 깊이탐색이 조금더 유리하다 고 알고있다.
지금이야 양이 적어서 그렇지만 양이 많아지면 길찾기 알고리즘을 좀 더 얹은 경우 DFS 가 더 유리하다고 한다.
아래는 코파일럿 한테 물어본 장점이다.
재귀 함수의 장점
- 코드의 간결성: 재귀 함수는 코드가 더 직관적이고 간결하게 작성될 수 있습니다. 특히 DFS의 경우, 재귀를 통해 깊이 우선 탐색을 구현하면 코드가 더 간결해집니다.
- 자연스러운 트리 구조 처리: 재귀 함수는 트리 구조를 처리할 때 자연스럽게 호출 스택을 활용할 수 있어, 트리 탐색에 특히 유리합니다.
- 구현의 용이성: 재귀를 이용하면 각 노드를 방문할 때마다 탐색 로직을 동일하게 적용할 수 있어, 구현이 상대적으로 간단합니다.
노드 방식의 장점
- 스택 오버플로우 방지: 큰 그래프나 트리를 탐색할 때, 재귀 함수는 호출 스택이 꽉 차서 스택 오버플로우가 발생할 수 있습니다. 노드 방식(큐나 스택을 직접 사용하는 방법)은 이러한 문제를 피할 수 있습니다.
- 메모리 사용 효율: 반복문과 큐 또는 스택을 사용한 노드 방식은 메모리 사용을 더 효율적으로 관리할 수 있습니다.
- 명시적 제어 흐름: 노드 방식은 탐색의 흐름을 명시적으로 제어할 수 있어, 디버깅이 용이합니다.
'IT > 학습' 카테고리의 다른 글
| 캡쳐 클로저 (1) | 2024.12.20 |
|---|---|
| Delegate와 Event (0) | 2024.12.20 |
| 링크드 리스트 (1) | 2024.12.19 |
| C# 콜렉션중 4가지를 마비노기에 빗대어 보자 (2) | 2024.12.16 |
| 추상 클래스와 인터페이스 차이 (0) | 2024.12.14 |



